아핀 변환이란?
- 기하학적 변환 중 하나로, 직선성과 평행성을 유지하면서 2D 또는 3D 공간의 점들을 변환하는 방식
- 이미지 처리, 컴퓨터 그래픽스, 로봇 공학 등에서 사용됨
아핀 변환이 포함하는 기본 변환들
아래와 같은 변환을 한꺼번에 또는 조합해서 적용할 수 있음
| 종류 | 정의 | 2D | 3D |
|---|---|---|---|
| 이동 (translation) | 물체를 x,y축 방향으로 옮김 | ||
| 회전 (rotation) | 어떤 기준점을 중심으로 회전시킴 | $\begin{bmatrix} cos(π/3) & −sin(π/3)\\ sin(π/3) & cos(π/3)\\ \end{bmatrix}$ |
$\begin{bmatrix} cos(π/3) & −sin(π/3) & 0\\ sin(π/3) & cos(π/3) & 0\\ 0 & 0 & 1\\ \end{bmatrix}$ |
| 확대/축소 (scaling) | 크기를 키우거나 줄임 | \begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix} |
\begin{bmatrix} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\\ \end{bmatrix} |
| 반사 (reflection) | 대칭 변환 | \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} |
\begin{bmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} |
| 왜곡 (shear) | 물체를 기울이는 변환 | \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} |
\begin{bmatrix} 2 & 1 & 0\\ 1 & 2 & 0\\ 0 & 0 & 1\\ \end{bmatrix} |
이때 이동을 표현하기 위해서는 덧셈이 필요하다. 즉 아래와 같은 덧셈 연산이 필요하다.

이는 (x,y)에 선형 변환 A를 적용한 뒤 x축으로 b_1, y축으로 b_2 만큼 이동시키는 식을 의미한다.
이때 행렬을 추가하여 이동을 표현하지 않고, 기존 벡터에 차원을 하나 더 추가하여 평행이동을 함께 표현할 수 있다.
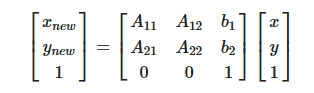
위와 같이 벡터의 방향, 크기, 위치 변화를 포함하는 변환을 아핀 변환 (Affine transformation)이라고 한다.
참고
아핀 변환 (Affine Transformation) - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
'Basic for AI > 통계 & 수학' 카테고리의 다른 글
| 수열과 점화식 (0) | 2023.08.10 |
|---|---|
| 피어슨 상관계수 (0) | 2023.07.10 |
| 정보이론(Information Content) (1) | 2023.07.06 |
| [선형대수학] 행렬 까먹은 내용 재정리 (0) | 2023.01.31 |
| 벡터의 선형종속과 선형독립, 기저 (0) | 2022.11.23 |


