수열과 점화식

수열과 점화식

학습 이유

데이터사이언스에서 연속적인 개념을 근사적으로 표현할 때 자주 등장

특히 수열의 점화식과 극한은 반복적이고 순차적인 데이터에 특화된 순환신경망 분석에서 매우 중요

---

수열(sequence)

정해진 규칙에 따라 차례대로 나열한 수

등차수열(arithmetic sequence)

두 항의 차가 일정한 수열

첫번째 항 a에 차례로 공차(common difference) d를 더해서 만든 수열

등차수열의 합인 등차급수

 

등비수열(geomoetric sequence)

두 항의 비가 일정한 수열

첫번째 항 a에 차례로 공비(common ratio) r을 곱해서 만든 수열

일반적으로 공비 r 은 0이 아니다.

 

등비수열 일반식

 

등비수열의 합인 등비급수

---

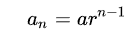
그외 수열들

자연수 거듭제곱의 합

---

수열의 점화식(recurrence formula)

주어진 수열 {a_n} 의 이웃하는 여러 항 사이의 관계식을 나타낸 것

 

유형 1. 연속된 두 수열의 차이가 어떤 수열인 점화식

점화식 유형1

이때 b_n을 계차수열(difference sequence), {a_n}을 계차수열을 갖는 수열(sequence with difference sequence)라고 한다.

 

n에 1부터 차례대로 대입한 뒤 양변을 모두 더하고 정리하면 일반항이 도출된다.

 

점화식 유형1의 일반항

---

유형2. 연속된 두 항의 비가 수열을 이루는 경우

점화식 유형2

n에 1부터 차례대로 대입한 뒤 곱하며 정리하면 일반항을 구할 수 있다.

유형2 일반항

---

유형3. 

점화식 유형 3

먼저 아래와 같은 형식으로 식을 바꾼다.

점화식 유형3의 변형

그리고 n=1부터 대입후 곱하여 정리하면 일반항을 구할 수 있다.

점화식 유형3 일반항

 

유형3 일반항 정리

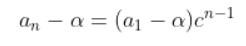
이때 alpha는 대입을 통해서 구할수도 있고, 아래 공식으로 구할수도 있다.

알파 구하는 공식