정보이론(Information Content)
추상적인 '정보'라는 개념을 정량화하고 정보의 저장과 통신을 연구하는 분야
정보를 정량적으로 표현하기 위한 세 가지 조건
1. 일어날 가능성이 높은 사건은 정보량이 낮고, 반드시 일어나는 사건은 정보가 없는 것이나 마찬가지다.
2. 일어날 가능성이 낮은 사건은 정보량이 높다.
3. 두 개의 독립적인 사건이 있을 때 전체 정보량은 각각의 정보량을 더한 것과 같다.
이러한 조건에 따라 아래 예제를 살펴보자
어떤 사람이 주머니에서 공을 꺼내는 과정을 반복하는 실험을 한다.

1. 각각의 주머니에서 공을 꺼낼 때 얻을 수 있는 정보량: 왼쪽 > 오른쪽
2. 파란색 공 999개와 빨간색 공 1개가 들어있는 주머니가 있을 때, 공을 하나 꺼내고 다시 넣는 실험을 반복한다.
이때 실험자는 주머니에 어떤 색깔의 공이 몇 개씩 들어 있는지 모르기 때문에, 공을 하나씩 뽑을 때마다 추측하는 확률 분포가 업데이트된다.
3. 파란색 공을 처음 몇 번 뽑았을 때 파란색 공을 뽑는 사건은 정보량이 높지만, 파란색 공만을 수십, 수백번을 뽑으면 파란색 공을 뽑는 사건의 확률이 1에 가깝기 때문에 큰 의미를 주지 못한다. 그러다가 하나 있는 빨간색 공을 뽑으면, 빨간 공을 뽑는 사건의 정보량은 매우 높다. 즉, 빨간색 공을 뽑기 전까지 관찰된 파란색 공의 수가 많을수록(즉 빨간색 공이 뽑힐 확률이 낮을수록) 빨간색 공을 뽑는 사건의 정보량은 높아진다.
정리하자면 발생할 확률이 높은 사건의 정보량은 낮고, 발생할 확률이 낮은 사건의 정보량은 크다고 볼 수 있다.
정보량(information content, I(x))
어떤 사건이나 정보가 가지는 정보의 양을 나타내는 척도
사건이나 정보가 발생할 때 그 사건이나 정보가 얼마나 놀라운가 또는 예상치 못한가에 따라서 결정됨
사건 가 일어날 확률을 라고 할 때, 사건의 정보량(information content) 는 다음과 같다.


정보량은 위의 "정보를 정량적으로 표현하기 위한 세 가지 조건"을 모두 만족한다.
b는 주로 2,e,10과 같은 값이 사용된다.
정보량은 하나의 사건에 대한 값을 의미한다. 그렇다면 여러 경우의 수가 존재하는 실험의 정보량은 어떻게 구할까?
확률변수가 갖는 모든 경우의 수에 대한 정보량을 구하고, 평균을 내면 확률 변수의 평균적인 정보량을 구할 수 있을 것이다. 이렇게 특정 확률분포를 따르는 사건들의 정보량 기댓값을 엔트로피(entropy)라고 한다. 엔트로피는 결국 정보량의 양을 측정하는 지표이며, 엔트로피가 높을수록 확률 분포의 불확실성이 높아져서 정보의 예측, 압축에 어려움을 준다.
엔트로피(entropy)
엔트로피는 어떤 시스템이 가지는 불확실성의 정도를 나타냄
시스템 내의 상태가 다양하고 복잡할수록 엔트로피가 높아지며, 상태가 단순하고 유일할수록 엔트로피가 낮음
확률 분포에 따라 계산되며, 각 사건에 대한 정보량을 가중평균하여 구함
이산확률 변수(Discrete Random Variables)의 엔트로피
각각의 경우의 수가 가지는 정보량에 확률을 곱한 후, 그 값을 모두 더한 값

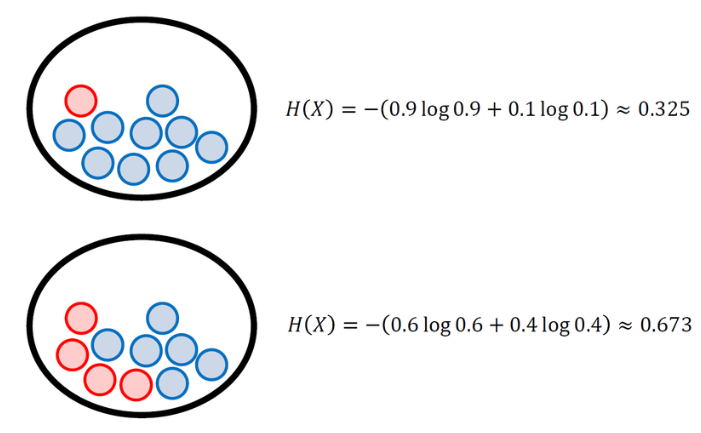
연속확률 변수(Continuous Random Variables)의 엔트로피
미분 엔트로피(differential entropy)라고도 불림
X가 연속확률변수인 경우, 이산 확률 변수때와는 다르게 적분의 형태로 정의된다.확률변수 X의 확률밀도함수가 p(x)일때, 엔트로피는 다음과 같다.
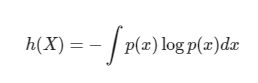
머신러닝의 목표는 모델의 확률 분포를 데이터의 실제 확률 분포에 가깝게 만드는 것이다.
머신러닝 모델은 크게 결정 모델(discriminative model)과 생성 모델(generative model)이 있다.
결정모델(discriminative model)
데이터의 실제 분포를 모델링 하지 않고 결정 경계(decision boundary)만을 학습
생성 모델(generative model)
데이터와 모델로부터 도출할 수 있는 여러 확률 분포와 베이즈 이론을 이용해서 데이터의 실제 분포를 간접적으로 모델링
생성 모델을 학습시킬 때는 두 확률 분포의 차이(실제 데이터의 분포와 모델이 예측한 분포의 차이)를 나타내는 지표가 필요
이러한 생성 모델 분포의 차이를 나타내는 대표적인 지표가 쿨백-라이블러 발산(Kullback-Leibler divergence, KL divergence)이다.
Kullback Leibler Divergence(KL divergence)
실제 데이터의 확률 분포 P(x)와 모델이 나타내는 확률 분포 Q(x)가 있다.
이때 두 분포의 KL divergence는 P(x)를 기준으로 계산된 Q(x)의 평균 정보량과, P(x)를 기준으로 계산된 P(x)의 평균 정보량의 차이이다.
즉 실제 확률 분포 대신 근사적인 분포 를 사용했을 때 발생하는 엔트로피의 변화량을 나타낸다.
머신러닝 모델에서는 KL divergence를 최소화하는 방향으로 모델을 학습시킨다
이산확률변수의 KL divergence
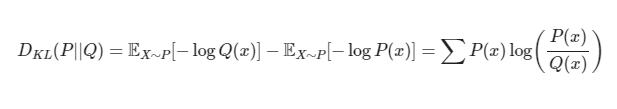
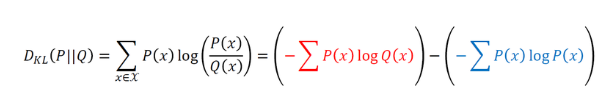
이산확률변수의 KL divergence를 구할 때 P(x)는 실제 데이터의 분포이므로 바꿀 수 없다. 따라서 위의 빨간색 식인 Q(x)에 대한 식을 최소화하는 문제, 즉 P(x)에 대한 Q(x)의 교차 엔트로피를 최소화하는 문제이다
또한 이러한 계산식으로부터 엔트로피, 교차 엔트로피, KL divergence 사이의 관계식을 얻을 수 있다.
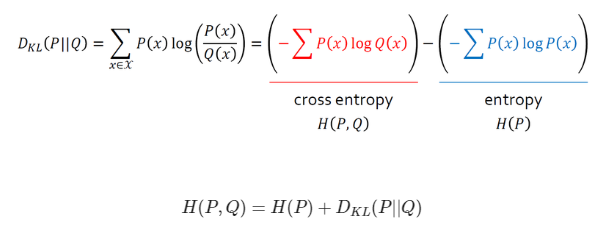
교차 엔트로피의 값이 작을수록 p와 q의 분포가 유사하며, 실제 분포와 가장 유사한 예측 분포를 찾는 것으로 판단할 수 있다.
연속확률변수의 KL divergence
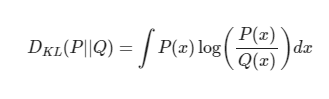
KL Divergence의 특성
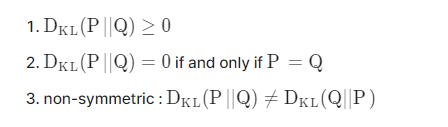
cross entropy loss
손실 함수의 한 종류
KL divergence를 최소화하는 것이 cross entropy를 최소화하는 것과 같다
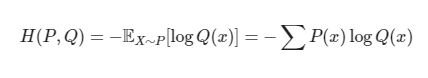
다중 분류 문제에서 softmax() 함수를 지난 출력값은 각각의 클래스에 속할 확률을 출력한다.
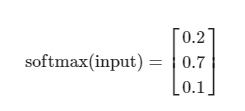
이 결과는 곧 다음 식과 같다.
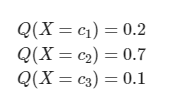
실제 label을 one-hot encoding하면 다음과 같다.
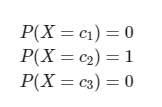
이러한 결과에 대해 cross entropy를 구할 수 있다.
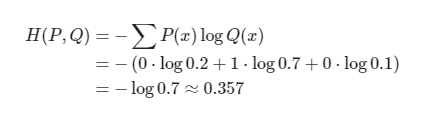
분류 문제에서는 데이터의 확률 분포가 one-hot vector로 표현되기 때문에, 분포 차이를 cross entroopy로 계산하면 계산이 계산 과정이 간단해진다는 장점이 있다.
cross entropy와 likelihood의 관계
모델의 파라미터를 θ라고 둘 때, cross entropy는 모델의 likelihood와 같다.
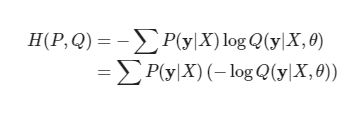
위의 식에서 바꿀 수 있는 부분은 부분 뿐이다.
따라서 cross entropy를 최소화하는 파라미터 값을 구하는 것은 결국 negative log likelihood를 최소화하는 파라미터를 구하는 것과 같다고 할 수 있다.
cross entropy의 사용처
cross entropy는 딥러닝의 분류 모델, 로지스틱 회귀 모델, decision tree계열 모델에서 loss 함수로 사용할 수 있다.
의사결정 트리는 가지고 있는 데이터를 특정 기준으로 나누고, 데이터를 나눴을 때 나누기 전보다 엔트로피가 감소하면 그만큼 모델 내부에 정보 이득(Information Gain) 을 얻었다고 본다.

는 라는 분류 기준을 선택했을 때의 엔트로피를 전체 사건 S의 엔트로피에 빼준 값, 즉 분류 기준 채택을 통해 얻은 정보 이득의 양을 말한다.
그러나 엔트로피가 낮은 쪽으로 분류를 진행한다고 해서 모델의 성능이 뛰어난 것은 아니다.
분명 엔트로피 기준으로는 더욱 정보 이득을 얻을 수 있음에도 불구하고 분류 기준을 더 세우지 않는 것이 전체 모델의 정확도 향상에 낫다. 계속해서 데이터 분류를 진행할 경우 decision tree의 depth가 너무 깊어져 Overfitting을 야기하기 때문이다.
decision tree의 depth를 결정하는 것은 실제 모델에서 depth만 바꿔서 모델 정확도를 확인해보는 식으로 결정할 수있다.
일반적인 가이드라인에서는 depth를 최대 5개로 제한한다.
이러한 decision tree의 문제를 해결하고자 다양한 분류 기준을 가진 Decision Tree 여러 개를 앙상블한 Random Forest 모델이 등장하였다.
예제 데이터로 decision tree 진행과정 알아보기
테니스 play에 대한 다음과 같은 데이터가 있다.
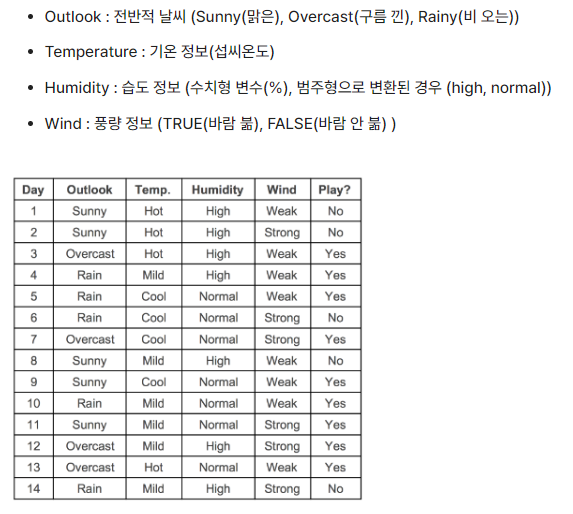
각 컬럼별 범주의 개수를 살펴보면
- outlook: sunny(5), overcast(4), rain(5)
- temp: hot(4), mild(6), cool(4)
- humidity: high(7), normal(7)
- wind: weak(8), strong(6)
- play(label): yes(9), no(5)
S라는 사건 집합이 가진 엔트로피, e(S)를 구해보자
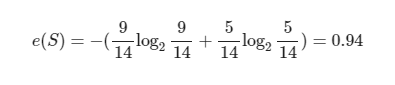
이제 각 feature에 대한 엔트로피를 각각 구하고 feature별 정보이득을 계산해서 가장 정보이득이 큰 순서대로 전체 사건을 2등분하며 분류를 수행한다.
사례이므로 F가 outlook 일때만 IG를 구해보자.
1. outlook 컬럼의 각각 범주별 엔트로피를 구한다.
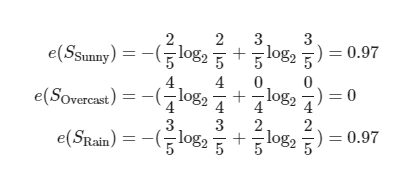
2. 정보 이득을 구한다.
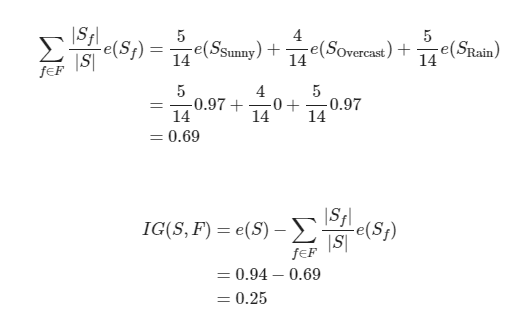
실습 문제
파란색 공 n개와 빨간색 공 1개가 있을 때, 빨간색 공을 뽑는 사건의 정보량을 구하는 코드를 작성하라
import numpy as np
import math
import random
# 주머니 속 공의 총 개수
n = 100
# 실험이 끝날 때까지 꺼낸 공의 개수
count = 1
while True:
sample = random.randrange(1, n+1)
if sample == n:
break
count += 1
print('number of blue samples:', str(count-1))
print('information content', str(-math.log(1/count)))'Basic for AI > 통계 & 수학' 카테고리의 다른 글
| 수열과 점화식 (0) | 2023.08.10 |
|---|---|
| 피어슨 상관계수 (0) | 2023.07.10 |
| [선형대수학] 행렬 까먹은 내용 재정리 (0) | 2023.01.31 |
| 벡터의 선형종속과 선형독립, 기저 (0) | 2022.11.23 |
| 01-1. 기본적 수학 개념 (0) | 2022.06.28 |

