데이터 전처리 기법들
전처리에서 해야할 일들
- 중복 데이터 제거
- 결측치 처리(제거 or 전치)
- 데이터 정규화
- 이상치 탐색 및 처리
- 구간화(binning)
- 범주형 데이터 원-핫 인코딩
- 연속형 데이터를 범주형으로 변환
그럼 이제 데이터 전처리의 각 주제에 대한 세부적 사항들을 살펴보자!
결측치 처리
데이터가 수치형 데이터냐, 범주형 데이터냐에 따라 처리 방법이 다르다.
# 결측치 여부 확인
df.isnull().any(axis=0)
# 결측치 개수 확인
df.isnull().sum()
# 결측치가 존재하는 행만 출력
df[df.isnull().any(axis=1)]
# 결측치 제거
df.dropna(how='all', subset=['컬럼명'], inplace=True)
수치형 데이터를 가진 컬럼의 결측치를 보완하는 방법
1. 특정값을 지정
2. 평균, 중앙값으로 대체
3. 다른 데이터를 이용한 예측값으로 대체
4. 시계열 특성을 가진 데이터의 경우 앞뒤 데이터를 통해 결측치 대체
아래 191번 인덱스를 가진 데이터를 4, 2번 방식으로 보완해보자

4월 앞뒤 월인 3월, 5월의 데이터셋 출력
trade[(trade['국가명']=='미국')&((trade['기간']=='2020년 03월')|(trade['기간']=='2020년 05월'))]
각 항목의 인덱스는 188, 194인 것을 알 수 있다.
191번 행의 결측치인 수출금액, 무역수지를 188과 194 행의 평균으로 채워보자
# 191번 인덱스의 '수출금액' 컬럼을 188, 194의 평균으로 대체
trade.loc[191, '수출금액'] = (trade.loc[188, '수출금액'] + trade.loc[194, '수출금액'] )/2
#191번 인덱스의 '무역수지' 컬럼을 188, 194의 평균으로 대체
trade.loc[191, '무역수지'] = (trade.loc[188, '무역수지'] + trade.loc[194, '무역수지'])/2
# 결과 확인
trade.loc[[191]]
#중앙값으로 채우기
# 전체 컬럼의 중앙값 계산
median_value = trade.median(axis=0)
# 191번 인덱스의 '수출금액' 컬럼을 전체 컬럼 중앙값으로 대체
trade.loc[191, '수출금액'] = median_value['수출금액']
# 191번 인덱스의 '무역수지' 컬럼을 전체 컬럼 중앙값으로 대체
trade.loc[191, '무역수지'] = median_value['무역수지']범주형 데이터를 가진 컬럼의 결측치를 보완하는 방법
1. 특정 값 지정('기타', '결측치' 등으로 채우기)
2. 최빈값으로 대체 (결측치가 많은 경우 지양할 것)
3. 다른 데이터를 이용한 예측값으로 대체
4. 시계열 특성을 가진 데이터는 앞뒤 데이터를 이용해 결측치 대체
중복 데이터 제거
같은 값을 가진 데이터 없이 행별로 값이 유일해야 한다면 중복 데이터를 제거해야 한다.
# 중복 데이터 여부 확인
trade.duplicated() # 중복 여부에 대한 T/F 반환
trade[trade.duplicated()] #중복되는 행 내용 출력
위 행과 중복되는 행을 전부 출력해보자
trade[(trade['기간']=='2020년 03월')&(trade['국가명']=='중국')]
위의 결과를 통해 인덱스 186, 187이 중복되고 있다는 걸 알 수 있다.
중복된 데이터를 pandas의 DataFrame.drop_duplicates() 함수를 이용해 제거하자
trade.drop_duplicates(inplace=True)
cf. drop_duplicates() 함수
- 판다스 라이브러리 함수로 데이터프레임의 중복값을 제거하는데 사용
- 기본적으로 중복값 중 인덱스가 작은 중복값을 제거(먼저 들어온 데이터)
- subset, keep(last, first), inplace, ignore_index 등의 파라미터 설정 가능
# df 데이터프레임의 id가 중복된 경우 나중에 들어온 값만 남기는 코드 작성
df.drop_duplicates(inplace=True, subset='id', keep='last')https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.drop_duplicates.html
pandas.DataFrame.drop_duplicates — pandas 2.0.2 documentation
next pandas.DataFrame.droplevel
pandas.pydata.org
이상치 처리
대부분 값의 범위에서 벗어나 극단적으로 크거나 작은 값
Min-Max Scaling을 했을 때 이상치는 1에 가까운 값을 갖는다,
몇 개의 이상치 때문에 대부분 값의 차이가 의미가 거의 없어지게 되므로, 극단적인 값이 생기는 경우를 제외하고 데이터를 고려하고 싶은 경우 이상치를 제거한다.
이상치 탐색(anomaly detection)
다양한 방법이 존재한다.
1. z score 방식
- 평균, 표준편차 이용
- 각 value에서 평균을 빼고 이를 표준편차로 나누어 z score를 계산한다
- z score가 특정 기준을 넘어가면 해당 데이터를 이상치라고 판단한다.
- 기준치를 얼마로 두느냐에 따라 이상치가 달라진다(z가 클수록 이상치 수가 적어짐)
- 정규분포를 따르는 데이터에 사용하기 좋다.
- z score 방식은 단점이 명확해 잘 사용하지 않는다
- Robust하지 못함
- 평균과 표준편차 자체가 이상치에 크게 영향을 받음
- 작은 데이터셋의 경우 z score로 이상치 알기 어려움. 특히 12개 이하인 경우 불가능
- Robust하지 못함
# z score로 이상치 구하는 함수
def outlier(df, col, z):
return df[abs(df[col] - np.mean(df[col]))/np.std(df[col])>z].index
# z=2일때 이상치로 분류되는 값 확인
trade.loc[outlier(trade, '무역수지', 2)]2. IQR 방식
- z-score의 대안적 방식
- 사분위 범위수(IQR) 사용
- IQR = Q3 - Q1
- 즉, IQR은 데이터의 중간 50% 범위를 의미
- 보다 왼쪽에 있거나, 보다 오른쪽에 있는 경우 이상치라고 판단
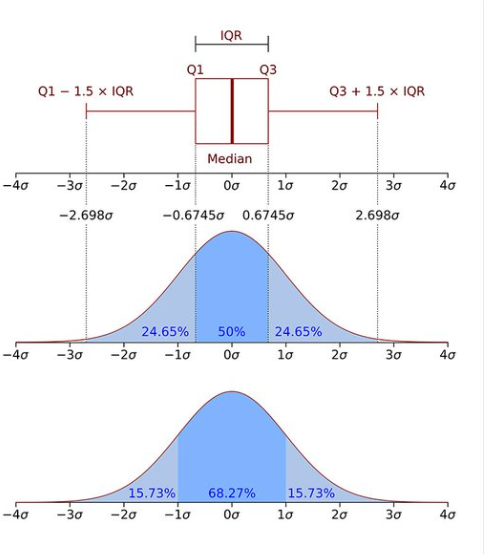
# IQR을 이용해 이상치를 탐색해보자
# 임의의 데이터 생성
np.random.seed(2020)
data = np.random.randn(100) # 평균 0, 표준편차 1의 분포에서 100개의 숫자를 샘플링한 데이터 생성
data = np.concatenate((data, np.array([8, 10, -3, -5]))) # [8, 10, -3, -5])를 데이터 뒤에 추가함
# 이상치 탐색
## 이상치: Q1 - 1.5*IQR 보다 작거나, Q3 + 1.5*IQR 보다 큰 값
Q3, Q1 = np.percentile(data, [75, 25]) # data 데이터셋의 백분위수 계산
IQR = Q3 - Q1
# 이상치 확인
print(data[(Q1-1.5*IQR > data)|(Q3+1.5*IQR < data)])
이상치 처리 방법
1. 이상치 제거
2. 이상치 대체: 데이터가 적은 경우
3. 다른 데이터를 이용해 예측 모델을 만들고 예측값을 활용
4. binning을 통해 수치형 데이터를 범주형으로 전환
정규화
수치형 데이터에서 각 컬럼마다 단위가 달라 스케일이 크게 차이가 날 경우, 머신러닝 모델 학습에 문제가 발생할 수 있다.
따라서 컬럼 간 범위가 크게 다를 경우 데이터 정규화를 통해 스케일을 유사하게 변경한다.
이때 train 데이터셋과 test 데이터셋 모두 같은 기준으로 정규화를 수행해야 한다!
이러한 정규화를 수행하는 방법은 매우 다양하다.
이 중 가장 잘 알려진 표준화(standardizaition), Min-Max Scaling을 알아보자.
cf. 정규분포 vs 표준정규분포
정규분포는 평균과 표준편차에 의해 모양이 결정되는 확률분포
표준정규분포는 평균이 0이고 표준편차가 1인 특별한 형태의 정규분포. 가우시안 분포라고도 불림.
그러면 어떤 데이터셋의 평균이 0이고 표준편차가 1이면 해당 데이터셋은 가우시안 분포를 따른다고 볼 수 있을까?
정답은 yes! (챗지피티가 그랬어요)
1. 표준화(Standardization)
데이터가 평균은 0, 분산은 1을 갖도록 변환
# 데이터 x를 Standardization 기법으로 정규화합니다.
x_standardization = (x-x.mean())/x.std()
# trade 데이터를 standardization 기법으로 정규화합니다.
cols = ['수출건수', '수출금액', '수입건수', '수입금액', '무역수지']
trade_standardization = (trade[cols]-trade[cols].mean())/trade[cols].std()
trade_standardization.head()
# 사이킷런을 이용해서 standarization 수행하기
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
# 훈련 데이터를 표준화
scaler.fit_transform(train)
# 테스트 데이터를 표준화
scaler.transform(test)
2. Min Max scaling
데이터의 최솟값은 0, 최댓값을 1로 갖도록 변환
피처의 범위가 다를 때 주로 사용하며 확률 분포를 모를 때 유용하게 사용
# 데이터 x를 min-max scaling 기법으로 정규화합니다.
x_min_max = (x-x.min())/(x.max()-x.min())
x_min_max
# trade 데이터를 min-max scaling 기법으로 정규화합니다.
trade[cols] = (trade[cols] - trade[cols].min()) / (trade[cols].max() - trade[cols].min())
trade.head()
# 사이킷런 라이브러리를 사용해 min max scaling 수행하기
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit_transform(train)
scaler.transform(test)
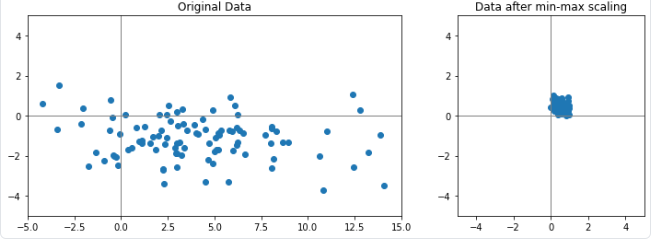
위의 예제 코드에서 사이킷런을 사용해 standardscaling과 min-max scaling을 진행하는 코드를 확인해보면, 변환(transform)을 진행할때, fit_transform과 transform 함수 2가지 종류를 사용하는 것을 확인할 수 있다.

그렇다면 fit_transform()과 transform() 함수의 차이점이 무엇일까?
"데이터셋에 정규화를 진행할 때, train 데이터셋과 test 데이터셋 모두 같은 기준으로 정규화를 수행해야 한다!"라는 점은 앞서 설명했던 내용이다. 즉, testset과 trainset에 Min-Max scaling을 수행할 경우 둘다 동일한 max값, min 값을 적용해야 하고, standardization을 수행할 경우 동일한 평균, 표준편차 값을 적용해야 한다는 것이다!
따라서 fit_transform(df)과 transform(df)함수는 모두 df에 대해 변환을 진행하지만, fit_transform()은 기준이 되는 값(위의 standarization의 평균, 표준편차나 min-max scaling의 min, max값)들을 저장해서 이후 transform() 함수를 사용할 때 해당 기준값을 사용하게 한다고 보면 될 것 같다.
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit_transform(train)
scaler.transform(test)
# quiz. 아래 ___에 들어갈 함수는?
scaler.___________(validation)그렇다면 위의 코드에서 validation dataset에 대해서도 추가적으로 정규화를 수행한다고 했을 때는 fit_transform()을 사용해야 할까? transform()을 사용해야 할까?
train dataset에 대해서 동일한 기준을 적용하여 정규화를 수행해야 하므로 transform()함수를 사용해야한다!
간략하게 정규화 진행시 fit_transform()은 기준점이고 한번만 사용되며, transform() 함수만 여러번 사용된다고 기억하면 될 것 같다.
원-핫 인코딩
카테고리별 이진 특성을 만들어 해당하는 특성만 1, 나머지는 0으로 만드는 방법
범주형 데이터를 다룰 때 사용
머신러닝, 딥러닝 수행시 범주형 데이터를 지원하지 않는 경우 원핫 인코딩을 수행하여 범주형 데이터를 사용해야 한다.
pandas를 활용해 손쉽게 one-hot encoding을 수행해보자
# get_dummies를 통해 trade 데이터프레임의 '국가명' 컬럼을 원-핫 인코딩을 수행해 새로운 데이터프레임 country 생성
country = pd.get_dummies(trade['국가명'])
country.head()
# concat으로 두 데이터프레임 병합
trade = pd.concat([trade, country], axis=1)
# 필요 없어진 '국가면' 컬럼 제거
trade.drop(['국가명'], axis=1, inplace=True)
trade.head()
구간화(binning, bucketing)
데이터를 구간별로 나누는 기법
연속적인 데이터를 구간으로 나눠 분석할 때 사용
# 구간 지정해서 나누기
bins = [0, 2000, 4000, 6000, 8000, 10000]
## cut() 이용해 데이터를 구간별로 분할
ctg = pd.cut(df[col], bins=bins)
ctg #pandas.core.series.Series 형태
## 구간별 값 수 확인
ctg.value_counts().sort_index()
# 구간 개수 지정해서 나누기
ctg = pd.cut(df[col], bins=6)
# 구간별 값 수 확인
ctg.value_counts().sort_index()
# qcut(): 구간을 일정하게 나누는 게 아니라 데이터 분포와 크기가 비슷한 그룹 q개로 나누어준다.
ctg = pd.qcut(salary, q=5) #그룹 5개이런 식으로 나뉘어진다.
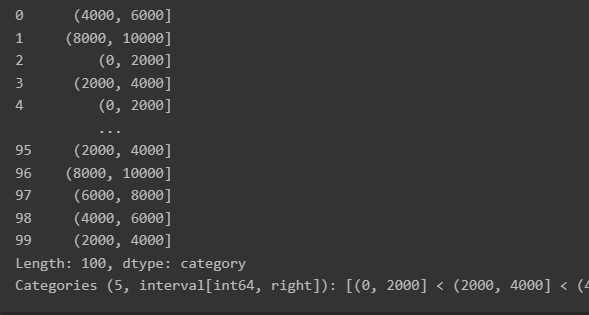
CF. 임베딩, 인코딩, 토큰화?
- 토큰화(Tokenization)
- 텍스트를 작은 단위로 나누는 과정
- "Hello, how are you?"라는 문장을 토큰화 >> "Hello", ",", "how", "are", "you "?"와 같은 단어 또는 기호
- 토큰화는 문장을 단어 또는 다른 단위로 나누기 때문에 문장을 이해하고 처리하기 쉬운 형태로 변환해줌
- 인코딩(Encoding):
- 인코딩은 토큰화된 단어 또는 문장을 수치화하는 과정
- 자연어 처리 모델은 텍스트를 수학적인 형식으로 표현할 수 있어야 함. 인코딩은 이를 가능하게 해주는 방법
- 일반적으로 각 토큰은 고유한 번호 또는 벡터로 매핑됨. 이를 통해 모델은 단어 또는 문장을 이해하고 처리할 수 있음
- 예를 들어, "Hello"를 1로, "how"를 2로, "are"를 3으로 인코딩하는 방식이 일반적
- 임베딩(Embedding):
- 임베딩은 단어나 문장을 저차원 실 벡터로 변환하는 과정
- 임베딩은 단어나 문장 간의 의미적 유사성을 보존하면서 벡터 공간상에 표현할 수 있게 함.
- 예를 들어, "cat"과 "dog"은 의미적으로 비슷한 단어들이기 때문에 벡터 공간에서 가깝게 표현될 것임
- 임베딩은 모델이 텍스트의 의미와 관계를 이해하고 유추하는 데 도움을 줌
- 임베딩은 자연어 처리 모델의 중요한 구성 요소로 활용되며, 예를 들어 단어 임베딩은 Word2Vec, GloVe 등의 알고리즘을 통 학습할 수 있습니다.
'AI Theory > key concept of AI' 카테고리의 다른 글
| 활성화 함수의 이해 (0) | 2023.07.03 |
|---|---|
| 딥네트워크 (0) | 2023.07.03 |
| 사이킷런 머신러닝 (0) | 2023.06.28 |
| 배열(array)과 파이썬 그래프 (0) | 2023.06.27 |
| 파이썬 더 잘 알기 (0) | 2023.06.26 |



