01. 확률이란
미래 사건의 발생에 관한 믿음의 척도
미래를 확실하게 예측할 수는 없지만, 오랜 시행에서 발생하는 상대도수가 대체로 매우 안정적인 성질을 갖는 사건들
02. 상호배반(disjoint, mutually exclusive)
두 집합 A, B에 대하여 A∩B = ∅ 인 경우 A,B는 상호배반이다.
03. 드 모르간의 법칙
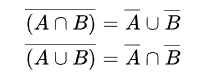
04. 집합의 분배법칙

05. 실험(experiment)
통제 여부와는 관계 없이 관측값을 생성하는 과정
06. 사건
실험이 실행될때 발생하는 하나 이상의 기본결과
07. 단순사건(simple event, E)
분해될 수 없는 사건
각 단순사건은 오직 하나의 표본점(E)에 대응한다.
반댓말: 복합 사건
08. 표본공간(sample space, S)
모든 가능한 표본점들로 구성된 집합
09. 이산표본공간(discrete sample space)
유한개이거나 셀 수 있는 서로 다른 표본점들을 포함하는 표본공간
10. 이산표본공간 S에 속하는 사건은 표본점들의 모임인 S의 임의의 부분집합이다.
11. 확률의 정의에 대한 기본 공리 3가지
표본공간 S에 속한 모든 사건 A에 대하여 다음 공리를 만족하는 A의 확률 P(A)를 할당한다
공리1: P(A) >= 0
공리2: P(S) = 1
공리3: S에 속하는 사건 A_1, A_2, ... A_n 가 상호배반일 경우,

12. 유한이거나 가산 집합의 표본점들을 포함하는 표본공간에서 정의된 사건의 확률을 구하는 방법
표본점 방법(sample point)
실험을 정의하고 하나의 단순사건을 설명하는 방법을 명확하게 결정
실험과 연관된 단순사건들을 나열하고 그것이 분해될 수 없음을 검사하라. 이것이 표본공간 S를 정의함
$$ S에 속하는 표본점들에 대하여 P(E_i) >= 0 이고 ∑P(E_i) = 1 를 만족하는 합리적인 확률을 할당 $$
표본점들의 특정한 모임으로 관심있는 사건 A를 정의
A에 속하는 표본점들의 확률을 더하여 P(A)를 구하라
사건-합성 방법(event composition)
13. 표본점들을 집계하는 방법
14. 조건부 확률
15. 독립(independent)
16. 확률의 곱셈법칙
17. 확률의 덧셈법칙
18. 분할(partition)
19. 베이즈 법칙
20. 확률변수(random variable)
21. 표본추출방법
비복원추출
복원추출
실험설계
22. 확률표본(random sample)